.
 

KOMBINASI

Kombinasi C dari sebuah himpunan S adalah himpunan bagian dari S.
C \subseteq S
Sebagai contoh, misalkan terdapat suatu kumpulan buah: apel, jeruk, mangga, pisang. Maka {apel, jeruk} dan {jeruk, mangga, pisang} adalah merupakan kombinasi dari kumpulan tersebut. Seluruh himpunan bagian yang mungkin dibentuk dari kumpulan buah tersebut adalah:

  • tidak ada buah apa pun
  • satu buah:
    • apel
    • jeruk
    • mangga
    • pisang
  • dua buah:
    • apel, jeruk
    • apel, mangga
    • apel, pisang
    • jeruk, mangga
    • jeruk, pisang
    • mangga, pisang
  • tiga buah:
    • apel, jeruk, mangga
    • apel, jeruk, pisang
    • apel, mangga, pisang
    • jeruk, mangga, pisang
  • empat buah:
    • apel, jeruk, mangga, pisang
Kombinasi r dari sebuah himpunan S, berarti dari himpunan S diambil elemen sebanyak r untuk dijadikan sebuah himpunan baru. Dalam hal kumpulan buah di atas, himpunan {apel, jeruk, pisang} adalah sebuah kombinasi 3 dari S, sedangkan {jeruk, pisang} adalah sebuah kombinasi 2 dari S.
Banyaknya kombinasi r dari sebuah himpunan berisi n elemen dapat dihitung tanpa harus memperhatikan isi dari himpunan tersebut. Besarnya dinyatakan dengan fungsi:
C_r^n = \frac{n!}{r!(n-r)!}
Fungsi C_r^n dalam banyak literatur dinyatakan juga dengan notasi {n \choose r}.
Sebagai contoh, tanpa harus mengetahui elemen himpunan {apel, jeruk, mangga, pisang}, banyaknya kombinasi 3 dari himpunan tersebut dapat dihitung:
C_3^4 = \frac{4!}{3!(4-3)!} = 4

Sifat rekursif dari Kombinasi

Kombinasi dapat dibentuk dari dua kombinasi sebelumnya. Ini mengakibatkan banyaknya kombinasi juga bersifat rekursif:
C^n_r = C^{n-1}_{r-1} + C^{n-1}_{r}

Hubungan dengan Permutasi

Dari himpunan {apel, jeruk, mangga, pisang} dapat diambil permutasi 3 unsur, yang dapat didaftar sebagai berikut:
apel jeruk mangga apel mangga jeruk jeruk apel mangga jeruk mangga apel mangga apel jeruk mangga jeruk apel
apel jeruk pisang apel pisang jeruk jeruk apel pisang jeruk pisang apel pisang apel jeruk pisang jeruk apel
apel mangga pisang apel pisang mangga mangga apel pisang mangga pisang apel pisang apel mangga pisang mangga apel
jeruk mangga pisang jeruk pisang mangga mangga jeruk pisang mangga pisang jeruk pisang jeruk mangga pisang mangga jeruk
Perhatikan bahwa dalam susunan ini setiap kolom merupakan permutasi dari kolom pertama. Karena dalam kombinasi urutan tidak dipentingkan, maka cukup salah satu kolom saja yang diambil. Jika kita mengambil kolom pertama saja, maka kita mendapatkan kombinasi 3 dari keempat buah tersebut adalah:
  • apel, jeruk, mangga
  • apel, jeruk, pisang
  • apel, mangga, pisang
  • jeruk, mangga, pisang
Penyusunan tabel seperti di atas akan menghasilkan P ^4_3 atau 24 permutasi, dengan 3! kolom, karena untuk setiap baris terdapat 3! permutasi dari kolom pertama. Dengan demikian, jumlah baris dari tabel akan sebesar:
\frac{P ^4_3}{3!}
Aturan seperti ini dapat digeneralisasikan sehingga untuk setiap n unsur yang dikombinasikan r unsur, berlaku:
C^n_r = \frac{P^n_r}{r!}
Yang dapat dengan mudah dibuktikan:
C^n_r = \frac{P^n_r}{r!}
= \frac{\frac{n!}{(n-r)!}}{r!}
= \frac{n!}{r! (n-r)!}

Hubungan dengan Permutasi Berunsur Identik

Kombinasi juga berhubungan dengan permutasi dengan unsur identik. Kombinasi dari sebuah himpunan S dapat dimengerti sebagai pemilihan unsur-unsur himpunan S. Unsur yang terpilih kita tandai dengan 1, dan yang tidak terpilih kita tandai dengan 0. Dengan demikian dari himpunan {apel, jeruk, mangga, pisang} tersebut, kita dapat mendaftarkan kombinasi-3 nya seperti ini:
Kombinasi apel jeruk mangga pisang
apel, jeruk, mangga 1 1 1 0
apel, jeruk, pisang 1 1 0 1
apel, mangga, pisang 1 0 1 1
jeruk, mangga, pisang 0 1 1 1
Dengan demikian, banyaknya kombinasi 3 unsur dari himpunan S yang berisi 4 benda setara dengan banyaknya permutasi terhadap untai 1110, yaitu:
\frac{4!}{3!} = 4
Karena untai 1110 memiliki 4 unsur, tetapi ada 3 unsur identik, yaitu 1. Maka total permutasinya adalah 4! dibagi dengan 3!. Kombinasi r dari n unsur, sesuai dengan pengertian itu, selalu setara dengan permutasi yang terdiri dari r angka 1 dan n - r angka 0. Maka permutasinya menjadi:
\frac{n!}{r! (n-r)!}
Yang sesuai dengan rumus kita di awal, untuk menghitung C^n_r.

Koefisien Binomial

Suatu binomial (a + b)n yang dijabarkan dalam bentuk jumlahan, akan membangkitkan koefisien-koefisien yang merupakan bilangan kombinasi.
(a + b)^n = \sum_{k = 0}^{n} {n \choose k} a^{n-k} b^k
Dengan penjabaran seperti di atas, maka banyaknya kombinasi r dari n unsur bisa didapat dari setiap suku:
{n \choose r} = \mbox{koefisien } a^{r} b^{n-r}
Daftar berikut menunjukkan beberapa penjabaran binomial:
  1. (a + b)0 = 1a0b0
  2. (a + b)1 = 1a1b0 + 1a0b1
  3. (a + b)2 = 1a2b0 + 2a1b1 + 1a0b2
  4. (a + b)3 = 1a3b0 + 3a2b1 + 3a1b2 + 1a0b3
  5. (a + b)4 = 1a4b0 + 4a3b1 + 6a2b2 + 4a1b3 + 1a0b4
  6. (a + b)5 = 1a5b0 + 5a4b1 + 10a3b2 + 10a2b3 + 5a1b4 + 1a0b5
  7. (a + b)6 = 1a6b0 + 6a5b1 + 15a4b2 + 20a3b3 + 15a2b4 + 6a1b5 + 1a0b6

Segitiga Pascal

Dengan menuliskan hanya koefisiennya saja, dari penjabaran binomial dapat kita peroleh:
  1. (a + b)^0 = 1a^0b^0 \rightarrow 1
  2. (a + b)^1 = 1a^1b^0 + 1a^0b^1 \rightarrow 1, 1
  3. (a + b)^2 = 1a^2b^0 + 2a^1b^1 + 1a^0b^2 \rightarrow 1, 2, 1
  4. (a + b)^3 = 1a^3b^0 + 3a^2b^1 + 3a^1b^2 + 1a^0b^3 \rightarrow 1, 3, 3, 1
Jika diteruskan, daftar koefisien ini akan membentuk susunan yang disebut sebagai Segitiga Pascal.
1
        1  1
       1  2  1
      1  3  3  1
     1  4  6  4  1
    1  5 10 10  5  1
   1  6 15 20 15  6  1
  1  7 21 35 35 21  7  1
 1  8 28 56 70 56 28  8  1
By: Unknown di 21.11
Mata Pelajaran:

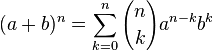
0 komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)