Trigonometri
Trigonometri (dari bahasa Yunani trigonon = tiga sudut dan metro = mengukur) adalah sebuah cabang matematika yang berhadapan dengan sudut segi tiga dan fungsi trigonometrik seperti sinus, cosinus, dan tangen. Trigonometri memiliki hubungan dengan geometri, meskipun ada ketidaksetujuan tentang apa hubungannya; bagi beberapa orang, trigonometri adalah bagian dari geometri.
Langganan:
Posting Komentar (Atom)






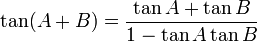


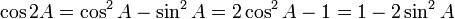




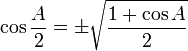
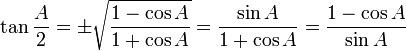


0 komentar:
Posting Komentar